目的

Atcoder ABC264に出場したので、その結果、感想、復習を兼ねて記事を書きました

atcoder.jp

解いたコードで、気になって色々修正もしたものは下記に置いてあります。動作確認済みです。

github.com

追記

UnionFindは、Unionする際に座標圧縮をしており、O(1) で find できているようです。unionする際に、rankで結合していないので、その分計算量は遅くなると思いますが。

algo-method.com

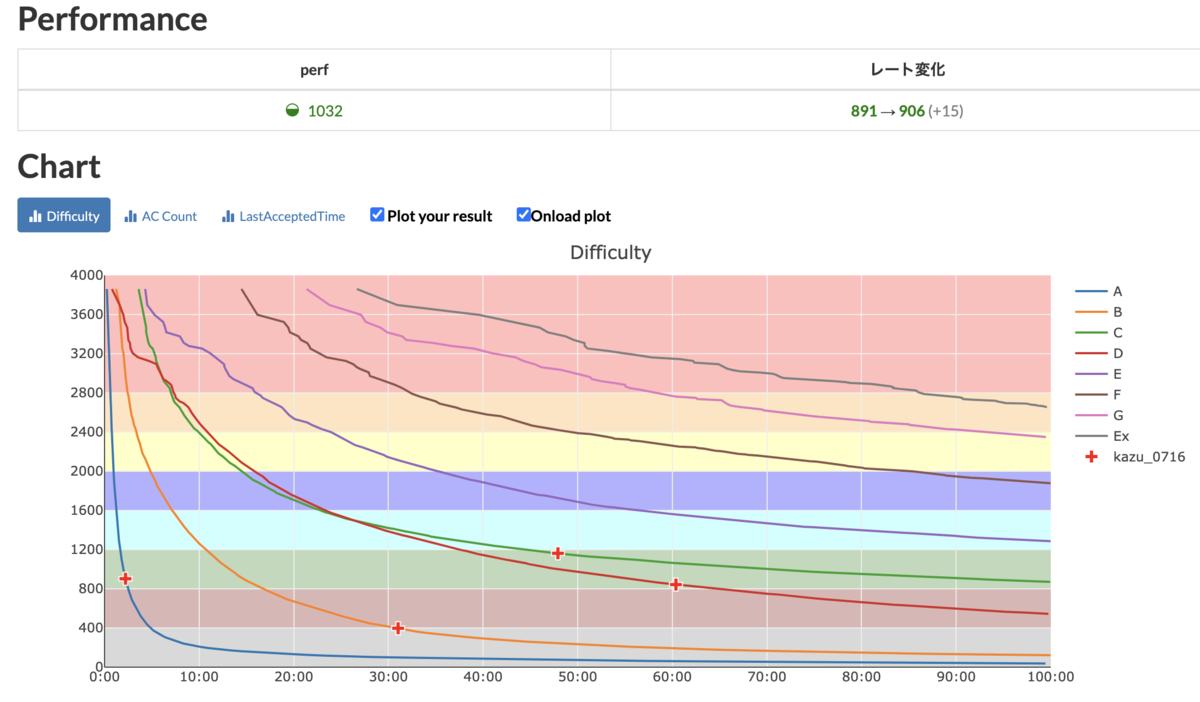
結果

ABCDの4問完で、E問題は方針はあってるものの、bugが取れずタイムアップしました。その後Dに取り組みましたが、途中まで間違った方針で解いていて、気づいた時には時遅しでタイムアップしてしまいました。

簡単なので、A問題は解答のみに留めます

atcoder.jp

B問題

15 * 15 マスのgridのうち(これは問題文より状態が与えられる)、R, C が与えられる(左上から初めて、縦 R 番目、横 C 番目)ので、それが何色か答える問題

atcoder.jp

考察

問題としては大きく2つの解き方があると思います。15 * 15 = 225(通り) なので、愚直に計算しても計算量としては問題ない量になります。

愚直に、15 * 15 のgridを描いて、R, C が何色か答える方法(ref: 公式解答2の方法)
法則を見つけて、R, C が何色かを1発で答える方法(ref: 公式解答1の方法)

自分は、2. の方針で解きましたが、ここで25分以上使ってしまい、後々解答時間が減っていってしまいました。

まず、 チェビシェフ距離 というものを知っていればよかったのですが、自分は知らずにここを0 から考えることになってしまったというのが2. で考える上では非常に厳しかったです。本来であれば、 1. で愚直に早く解いて次に行くべきでしたが、気がついたら多くの時間を使ってしまっていました。

ja.wikipedia.org

色々試行錯誤しましたが、中心の白い点(R, C) = (8, 8) の点を中心に(左上の点を (1, 1) だと考えた場合 ) 考えていくことに辿り着きました。 x, y = abs(R-8), abs(C-8) で考えると、中心を原点とみなした場合に、第一象限のみを考えればいいということがわかります(それぞれ対象で同じ法則で色が決まるので)。また、y = x の線を引くと、第一象限の中でも、線対象になっていることがわかります。

従って、中心からの縦の距離(abs(R - 8))、横の距離(abs(C - 8)) を考えた際にそれぞれの値の偶奇を考えれば、色がわかるということに辿り着きました

R, C = map(int, input().split())
if (R, C) == (8, 8):
    print("white")
else:
    dr, dc = abs(R-8), abs(C-8)
    if dr <= dc:
        # NOTE: 横長の場合は、横の距離で判定する
        print("white" if dc % 2 == 0 else "black")
    else:
        # NOTE: 縦長の場合は、横の距離で判定する
        print("white" if dr % 2 == 0 else "black")

atcoder.jp

コンテスト後にリファクタリングしましたが、上記のコードは下記のようにもっと簡単にすることができます。

atcoder.jp

これにより、時間内に問題を解くことができました。

C問題

任意の2次元配列A, Bが与えられ(サイズはBの方がAよりも小さい)、Aのうち任意の行/ 列を削除した際に A = B にすることができるか

atcoder.jp

考察

Aの配列のうち、縦から H2個、横から W2個それぞれ選んで2次元配列A' を作り、それがBと一致するか？を考えました。 H1, H2 <= 10 のため、組み合わせを考えても (10C5) ^ 2 = (252) ^ 2 < 90,000(= 300 ^ 2) なので、十分計算できると考えました。 python だと from itertools import combinations で組み合わせの場合のtupleを返してくれる組み込み関数があるので利用しました。ない場合は、再帰などを用いて求めることになると思います。

from itertools import combinations

H1, W1 = map(int, input().split())
A = [list(input().split()) for _ in range(H1)]
H2, W2 = map(int, input().split())
B = [list(input().split()) for _ in range(H2)]

for hc in combinations(range(H1), H2):
    for wc in combinations(range(W1), W2):
        flags = True
        for i, h in enumerate(hc):
            for j, w in enumerate(wc):
                if B[i][j] != A[h][w]:
                    flags = False
        if flags:
            print("Yes")
            exit()
print("No")

atcoder.jp

2重ループのうち、途中で違ったらbreakした方が早いので、コンテスト後に下記のようにリファクタリングしました(9 msしか差がないので微妙なところですが)。

atcoder.jp

公式解説ですと、bit全探索で (2 ^ 10) ^ 2 = 1,048,576 通りを全探索していますが、これでも十分間に合います。ただ、Aうちで、選ぶ行/ 列は Bの縦/ 横の大きさと同等のため、無駄に探索することになり計算量が大きくなってしまいます。

atcoder.jp

D問題

"atcoder" という文字列を並び替えられた入力 S を、何回隣り合った文字を交換することで "atcoder" に戻せるか。最小の交換回数を求めよ。

atcoder.jp

考察

解説を見ると、「転倒数」という問題を知っていれば、O(nlogn) で解くことができます。

atcoder.jp

ただ、自分は知らずに、BIT(Binary Indexed Tree) もライブラリとして持っていないので、バブルソート(O(n²)) を実装する形で解きました。

ja.wikipedia.org

今回は、 "atcoder" = 7文字だったので、O(n²) でも十分解くことができました。しかし、文字数(それぞれユニークであることが必要だが)がより長くなる場合には、解くことができません。また、バブルソート的にswapした回数が最小になるか？に関しても確信はないまま(まぁ、たぶん大丈夫だろう)という気持ちで提出しました。

scrapbox.io

S = list(input())
target, ans = list("atcoder"), 0
while S != target:
    for i in range(len(S)-1):
        cur, nxt = S[i], S[i+1]
        if target.index(cur) > target.index(nxt):
            S[i], S[i+1] = nxt, cur
            ans += 1
print(ans)

atcoder.jp

コンテスト後に、stringで都度index取る方法だと効率悪いので、dict(辞書型、他の言語で言う連想配列(= hashmap)) で解く方法にリファクタリングしました。

atcoder.jp

E問題

N + M 個の node と、E 本の辺が与えられる
- 1~N 番目の node は街で、 N + 1 番目 ~ N + M 番目のノードは発電所
1つの辺を切っていく(X個の辺を最終的に切る)
- 発電所につながっている node は電気が通っている
- 電気が通っている街の数を常に出力せよ

atcoder.jp

考察

まず、問題を読んでUnionFind Tree(以下、UnionFind)を使って解くことを考えました。これは、「根を持つ木」を高速に生成でき、根が発電所であればOK(電気が通っている)、そうでない場合は NG(電気が通っていない)と考えました。

ja.wikipedia.org

ここで、UnionFind の性質と、発電所が N + 1 番目以降の node である問題特性から 2 つのポイントがあったと考えます。

UnionFind では、2つの木を結合(Unionする)ことはできるが、分割はできないので、全て辺が切れてしまっている状態から、結合していくのがよい(= 逆から見る)
結合した根は、必ずindex番号が大きいものになるように工夫する必要がある(= 発電所かどうか判定するため)

また、都度出力する必要があるので、その際にどのように考えればいいかと、下記の2パターンになる。最初に、電気が通っている街がいくつあるのか？は、O(NlogN)程度で求められると考え(全ての街の親nodeを調べて、親が発電所であれば+1する)、その後辺を突合するたびに街の数を加算していく & その数を配列に保持し、最後に逆順序にして出力すればいいと考えました。

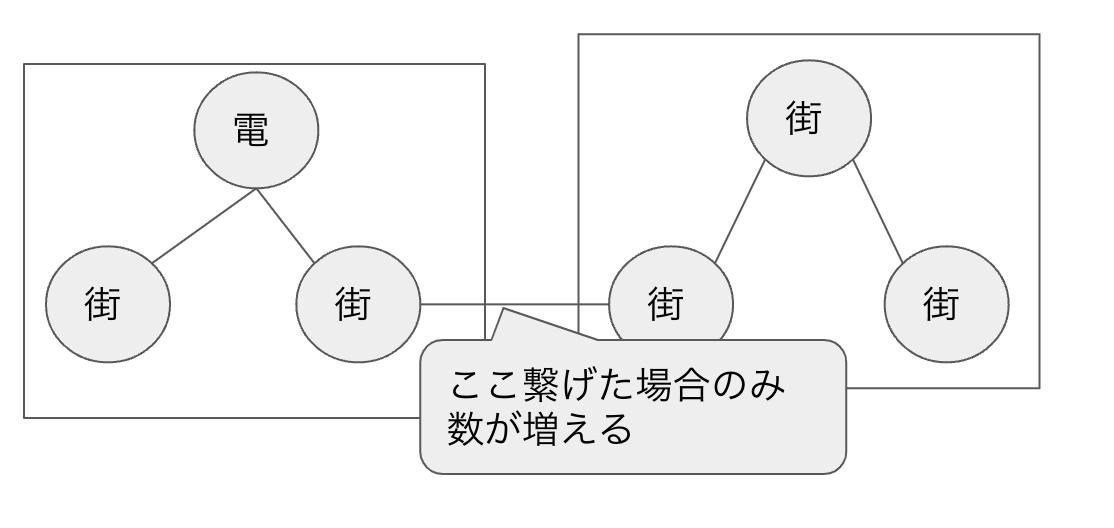
繋げるそれぞれの木の根が、両方発電所、もしくは両方街の場合は、電気が通っている街は変わらない
繋げるそれぞれの木の根が、どちらか発電所の場合は、根が街の木の大きさ分(= 街の数)加算する

ちなみに、下記の実装にもありますが、木の大きさは O(logN) 程度で求められると考えられる(findがO(logN)で、見つけた親のsizeを求めるのは、配列へのアクセスなのでO(1))ので、なんとか間に合うのではないか？と考えました。ここのサイズの大きさをどう求めるか？に関しては知らなくてコンテスト中に調べて辿り着きました。

note.nkmk.me

ただ、時間内には下記の方法で実装したものの、サンプルと答えが合わず、残り時間もなくてタイムアップしてしまいました。

from collections import defaultdict


class UnionFind():
    def __init__(self, n):
        self.n = n
        self.parents = [-1] * n

    def find(self, x):
        if self.parents[x] < 0:
            return x
        else:
            self.parents[x] = self.find(self.parents[x])
            return self.parents[x]

    def union(self, x, y):
        x = self.find(x)
        y = self.find(y)

        if x == y:
            return

        if self.parents[x] < self.parents[y]:
            x, y = y, x

        self.parents[x] += self.parents[y]
        self.parents[y] = x

    def size(self, x):
        return -self.parents[self.find(x)]


N, M, E = map(int, input().split())
conn = defaultdict(tuple)
for i in range(E):
    U, V = map(int, input().split())
    conn[i] = (U-1, V-1)
Q = int(input())
dis_conn = []
for _ in range(Q):
    X = int(input())
    dis_conn.append(conn[X-1])
    del conn[X-1]
uf = UnionFind(N+M)
for k in conn:
    uf.union(conn[k][0], conn[k][1])
cnt = 0
for i in range(N):
    if uf.find(i) >= N:
        cnt += 1
ans = [cnt]
while dis_conn:
    u, v = dis_conn.pop()
    u_par, v_par = uf.find(u), uf.find(v)
    if (u_par < N and v_par < N) or (u_par >= N and v_par >= N):
        pass
    elif u_par >= N and v_par < N:
        cnt += uf.size(v)
    elif u_par < N and v_par >= N:
        cnt += uf.size(u)
    ans.append(cnt)
    uf.union(u, v)
print(*ans[::-1][1:], sep="\n")

結論言うと、UnionFind の union 関数に間違いがあり、if self.parents[x] < self.parents[y]: ではなく if x < y: とすべきでした。大元のライブラリでは、木のnode数で比較していたのに気づかず、雑に書き換えてしまったのが原因でした。そのため、unionした際に、根がindex番号が必ずしも大きいものにならず、発電所が木の中にあっても、根にならないパターンを生み出してしまい、答えが合わなかったです。

atcoder.jp

コンテスト後は上記のように修正し、無事問題を解くことができました。

感想

結果として、4完し緑パフォでrateが若干上がりましたが、E問題ほぼ解けていたのにも関わらず、落としてしまい自分としては悔いの残る形になりました。

特に、B問題までに時間かけすぎており、ここを高速化することで今後はrateが上がることが期待できるので、愚直に綺麗でなくても解くことをする。そして、DやEで出る水色下位(1400 diff以下)の問題を解くことでrateをさらに上げることができると思うので、引き続き精進していければいいなと思いました。

水色はまだまだ先として、早くコンテスト中にE問題解けるようになりたいな。